Chiffre de Porta/Bellaso et chiffre de Vigénere

Giovanni Battista Della Porta est un savant, philosophe, physicien et bien sûr cryptologue italien du XVI ème siècle. (durant la renaissance italienne). Dans son livre intitulé "De Furtivis Literarum Notis", paru en 1563, Porta donne une nouvelle méthode de chiffrement utilisant deux alphabets (polyalphabétique) et une clé de chiffrement. Cette méthode est à l'origine de tous les cryptages polyalphabétiques ou utilisant une clé. L"invention de ce système ne provient pas exactement de Porta mais plutôt du cryptologue Giovan Battista Bellaso qui le produisit 30 ans plus tôt. Mais ce dernier étant bien moins réputé que Porta, le système de codage garda principalement le nom de Porta.
Fonctionnement
Pour coder un message grâce au code de Porta/Bellaso il faut une clé de chiffrement prédéfinie par l'expéditeur et que le destinataire du message connaît.
On associe ensuite à chaque lettre du message codé une des lettres de la clé dans l'ordre et si le message est plus long que la clé alors la clé est répétée autant de fois que nécessaire :
Exemple : Message à coder : Porta a volé le code de Bellaso
Clé : cryptologie
On asssocie aux lettres du message une des lettres de la clé (dans l'ordre) :
P O R T A A V O L E L E C O D E D E B E L L A S O
C R Y P T O L O G I E C R Y P T O L O G I E C R Y
Il faut ensuite utiliser le tableau de Porta/Bellaso (adapté à l'alphabet contemporain car au XVI ème siècle les lettres J, K, U et W n'existaient pas) :
Tableau original de Bellaso
Lettres de la clé Lettres du message


Pour coder le message voulu on regarde la lettre de la clé associée à la première lettre du message. Pour notre exemple la lettre de la clé associée au P du message est la lettre C.
On prend la ligne dans laquelle se trouve la lettre C de la première colonne (deuxième ligne).
On prend ensuite la première lettre du message (P) et on lui associe la lettre en face dans la ligne choisie (D)
Ainsi le P est codé D.
On trouve enfin le :
DJDAR T AIVN WQ UAWV WZ UOUWZAA
Pour déchiffrer ensuite notre message codé il suffit de faire l'inverse (à condition de connaitre la clé).
On regarde la première lettre de la clé dans la première collonne (ici le C) puis on regarde quelle lettre est en face de celle du message codé (ici le D est en face du P ). ainsi dans notre message codé le C signifie P dans notre message initial.
On fait de même pour toutes les lettres du message codé jusqu'à obtenir notre message initial :
Porta a volé le code de Bellaso
avec la clé : cryptologie
Casser le code
Pour casser le code de Porta/Bellaso il faut utiliser la même technique que pour le chiffre de Vigenère, cette méthode est expliquée plus bas à la suite de l'explication du chiffre de Vigenère.
Exercice :
Essayez, avec le chiffre de Porta/Bellaso, de coder la message : LA CRYPTOLOGIE EST UN ART avec la clé : PORTA
Puis essayez de décoder le message suivant : ZYQK NDMFT MFR BVVPFXR avec la clé : BELLASO
Chiffre de Vigenère

Blaise de Vigenère, est un diplomate, astrologue, cryptologue et alchimiste français du XVI ème siècle. Ayant reçu une éducation solide et poussée parce qu'issu d'une famille noble, il se retrouve à Paris où il va vivre de nombreuses expériences avec des personnes connues. En 1569, il se trouve a Rome et lit de nombreux ouvrages de crytpographie. Il s'inspire notamment de l'ouvrage de Porta dans lequel il prend connaissance du chiffre de Porta/Bellaso.
Il va ensuite publier son propre livre de cryptologie en 1586 intitulé :"traité des chiffres" dans lequel il présente sa propre méthode de cryptage appellée "chiffre de Vigenère" inspiré du travail de Bellaso.
Fonctionnement
Tout d'abord, pour utiliser le chiffre de Vigenère, il faut un outil indispensable : La table de Vigenère :

Le codage grâce au chiffre de Vigenère est assez semblable à celui de Porta/Bellaso.
Pour coder une lettre il faut la remplacer par la lettre qui se trouve a l'intersection entre la colonne de la première lettre du message et la ligne de la première lettre de la clé.
Exemple :
On souhaite coder le message : "Vigenère était un grand savant" avec la clé : cryptologie
On prend la colonne qui contient la première lettre du message (V) et la ligne qui contient la première lettre de la clé (C). La lettre à l'intersection est un X. Ainsi la lettre V du message est codée "X".
On fait cela pour toutes les lettres du message en recommençant au début de la clé lorsque la dernière lettre a été utilisée jusqu’à obtenir un message complètement crypté grâce au chiffre de Vigenère :
Xzetgscs kbekk sc zflbj aexrli
Pour décoder le message il suffit de faire marche arrière (à condition de connaître la clé) : On prend la ligne de la première lettre de la clé et on avance sur cette ligne jusqu'à trouver la première lettre du message codé. On regarde ensuite la lettre se trouvant dans cette colonne : c'est la première lettre du vrai message.
Exemple : on souhaite décoder le message suivant :
"Xzetgsc szimv rshlw owvtsorrt" avec la clé "cryptologie"
On prend la ligne du C et on avance sur cette ligne jusqu'à trouver la lettre X. Cette colonne correspond à la lettre V. Ainsi la première lettre du message de départ est un V.
On fait de même avec les autres lettres du message codé et de la clé jusqu'à obtenir le message décrypté : Vigenère était aussi diplomate.
Casser le chiffre de Vigenère
Le chiffre de Vigenère est resté longtemps intact malgrè les nombreuses attaques des cryptanalystes qui souhaitaient casser une fois pour toute le chiffre de Vigenère considéré jusque là comme inviolable.
Mais au XIX ème siècle, le chiffre de Vigenère a enfin été cassé pour la première fois rendant l'utilisation de ce chiffre peu sûre.
Pour casser le code de Vigenère il, faut d'abord trouver la longueur de la clé puis
ensuite trouver les lettres qui la composent. Une fois la clé découverte le message peut être déchiffré normalement.
Pour trouver la longueur de la clé il existe deux méthodes :
La méthode de Charles Babbage :
Charles Babbage, fils d'un banquier londonien, a fait de nombreuses découvertes scientifiques au XIX ème siècle. Il s'intéresse aux statistiques et au calcul des coordonnées pour ensuite se plonger dans la cryptologie.
Aux alentours de 1850, il propose une technique efficace qui permet de casser le chiffre de Vigenère, technique qui a été retrouvée par un officier prussien à la retraite, Friedrich Wilhelm Kasiski, en 1863.
Cette technique vient du fait que Babbage a remarqué que dans certains longs textes cryptés par un chiffre de Vigenère, certains groupes de lettres réapparaissent plusieurs fois dans le texte.
Exemple :
KQOWE FVJPU JUUNU KGLME KJINM WUXFQ MKJBG WRLFN FGHUD WUUMB SVLPS NCMUE KQCTE SWREE KOYSS IWCTU AXYOT APXPL WPNTC GOJBG FQHTD WXIZAYGFFN SXCSE YNCTS SPNTU JNYTG GWZGR WUUNE JUUQE APYME KQHUI DUXFP GUYTS MTFFS HNUOC ZGMRU WEYTR GKMEE DCTVR ECFBD JQCUS WVBPN LGOYL SKMTE FVJJT WWMFM WPNME MTMHR SPXFS SKFFS TNUOC ZGMDO EOYEE KCPJR GPMUR SKHFR SEIUE VGOYC WXIZA YGOSA ANYDO EOYJL WUNHA MEBFE LXYVL WNOJN SIOFR WUCCE SWKVI DGMUC GOCRU WGNMA AFFVN SIUDE KQHCE UCPFC MPVSU DGAVE MNYMA MVLFM AOYFN TQCUA FVFJN XKLNE IWCWO DCCUL WRIFT WGMUS WOVMA TNYBU HTCOC WFYTN MGYTQ MKBBN LGFBT WOJFT WGNTE JKNEE DCLDH WTVBU VGFBI JG
On remarque que dans ce texte certains groupes de lettres plus ou moins longs reviennent deux fois. On les classe ensuite selon un tableau comme celui qui suit :


Des répétitions de groupes de lettres correspondent souvent à des petits mots répétés plusieurs fois dans le message initial et crypté avec la même partie de la clé à plusieurs reprises. Cela arrivent souvent avec des petits mots tels que "et", "des", "mais" ...
Ainsi, entre ces répétitions, l'espace entre deux groupes correspond à la clé, une ou plusieurs fois de suite.
Il faut donc trouver le diviseur commun à tous les intervalles entre tous ces groupes de mots.
Pour notre exemple nous trouvons le diviseur 5. On peut donc fortement penser que la clé est constituée de 5 lettres.
Méthode de Friedman
William Friedman était un cryptologue américain qui faisait partie de l'armée de terre. Il a servi lors de la première guerre mondiale tout d'abord comme cryptologue. Il s’attaquait aux codes allemands et formait des officiers au cryptage puis il a été recruté comme soldat.
Il a ensuite servi lors de la seconde guerre mondiale en essayant de déchiffrer les messages cryptés japonais ( avec le code 97).
Il a aussi travaillé pour la NASA où il a été cryptologue en chef.
En 1920, Friedman publie un article dans lequel il montre comment il a calculé ce qu'il a appelé "l'indice de coïncidence". Cela correspond à la probabilité que deux lettres choisies aléatoirement soient les mêmes.
Il le calcule grâce à la formule suivante :
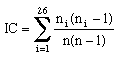
ou n = nombre de lettres dans l'alphabet et n1 = le nombre de fois la lettre A
n2 = le nombre de fois la lettre B
etc ....

Ainsi en calculant l'IC (indice de coïncidence) de plusieurs textes contemporains longs et en faisant la moyenne de leur IC, il calcule l'IC moyen des langues :

On a pu calculer qu'un alphabet aléatoire (où chaque lettre a la même chance de sortir) a un IC d'environ 0.038 tandis qu'un alphabet non aléatoire a un IC supérieur à 0.06.
Pour trouver la longueur de la clé, il faut découper le texte en plusieurs textes ne comportant qu'une partie des lettres du message (une lettre sur deux, une lettre sur trois etc....)
Exemple :
Nous allons découpé notre message en différents intervalles :
chaine 1 : KQOWE FVJPU JUUNU KGLME KJINM WUXFQ M... (intervalle de 1 = texte original)
chaine 2 : KOEVP JUUGM KIMUF M... ; QWFJU UNKLE JNWXQ... (intervalle de 2)
chaine 3 : KWVUU KMJMX M... ; QEJJN GEIWF...; OFPUU LKNUQ (intervalle de 3)
etc ........
On calcule ensuite les IC des sous-chaînes :

On observe que les Indices de coïncidences du texte coupé en intervalles de 5 se rapprochent plus de 0.074 (supérieur a 0.06) tandis que les IC des autres intervalles se rapprochent plus de 0.038.
On peut donc supposer que la clé utilisée pour chiffrer le message est de 5 lettres.
Décoder le message
Une fois la longueur trouvée, on peut maintenant décoder le message.
On sait que la clé a une longueur de 5 lettres. Ainsi les lettres 1,6,11,16,21 etc ... du message ont été codées avec la même lettre de la clé (la première).
On range ainsi toutes les lettres du messages qui ont été codées par la même lettre de la clé ensemble.
On peut ensuite effectuer une analyse de fréquence sur chaque groupe pour trouver le décalage utilisé et ainsi trouver la lettre de la clé qui correspond.
Exemple :
On prend les lettres du message qui ont été codées avec la première lettre de la clé :
KFJKK WMWFW SNKSK IAAWG FWYSY etc ....
La lettre qui revient le plus dans ce groupe de lettres est le W. On peut donc supposer que le W code la lettre E. On regarde ensuite dans le tableau de Vigenère la lettre de la clé dont le croisement avec la lettre E du message donne la lettre codée W : c'est le S.
Il y a fort à parier que la première lettre de la clé est un S.
On fait ensuite de même avec les lettres 2,7,12,17 ... ; 3,8,13,18,23 ...; 4,9,14,19... et 5,10,15,20 ...
On trouve enfin la clé qui est "SCUBA".
Un fois la clé trouvée il suffit de faire le chemin inverse du codage grâce au tableau de Vigenère.
On trouve enfin le message initial :
"Souvent pour s'amuser les hommes d'équipage prennent des albatros, vastes oiseaux des mers, qui suivent, indolents compagnons de voyage, le navire glissant sur les gouffres amers. A peine les ont-ils déposés sur les planches que ces rois de l'azur, maladroits et honteux, laissent piteusement leurs grandes ailes blanches, comme des avirons, traîner à côté d'eux. Ce voyageur ailé, comme il est gauche et veule, lui naguère si beau, qu'il est comique et laid. L'un agace son bec avec un brûle-gueule, l'autre mime en boitant l'infirme qui volait. Le poète est semblable au prince des nuées, qui hante la tempête et se rit de l'archer.
Baudelaire"
Mais ces techniques pour casser un chiffre de Vigenère ne marchent pas pour tous les textes, il faut que la clé ne dépasse pas la moitié du texte sinon les répétitions n'apparaissent plus et ces techniques subissent aussi les contraintes de l'analyse de fréquence.
Variante : le chiffre de Vernam
A la suite de la cryptanalyse du chiffre de Vigenère, l’ingénieur Gilbert Vernam a créé une variante du chiffre de Vigenère : le chiffre de Vernam ou masque jetable.
Le système est le même que le chiffre de Vigenère sauf que la clé doit être de même longueur que le message, absolument aléatoire et utilisée une seule fois.
Si l'on prend le message "vernam est très fort "
avec la clé : "jalghs orb dizp qmgh" (de même taille que le message et aléatoire)
On obtient le message codé : EECTH ESJUW ZDHVA XA
Un masque jetable est incassable par la force brute car il est impossible de trouver la clé et un même message peut vouloir dire des choses différentes en fonction de la clé.
Exemple :
Le message codé : "WMS" peut vouloir dire "OUI" avec la clé "HRJ" ou peut vouloir dire "NON" avec la clé "QBU".
Mais la difficulté de ce système repose sur le fait qu'il est difficile de faire des clés complètement aléatoires, qu'il ne faille pas réutiliser une clé déjà utilisée et qu'il faille a chaque message envoyé, envoyer la clé au destinataire afin qu'il puisse décoder le message. Ce sont ces échanges de clés qui rendent le système moins fiable et compliqué a utiliser.
Utilisations
On retrouve des traces d'utilisation du chiffre de Vigenère et du code de Porta/Bellaso dans les écrits sur la stratégie des pays au XVI ème siècle mais ils sont peut nombreux.
Le chiffre de Vernam a été utilisé par les américains et les russes dans leurs échanges via le téléphone rouge (téléphone direct entre les Etats-Unis et la Russie). Ils échangeaient des séries de clés via des "mallettes diplomatiques" dites inviolables et pouvaient ensuite s'envoyer des messages codés grâce aux clé échangées précédemment.
Il a aussi été utilisé par le KGB (service de renseignement russe) lors de la guerre froide mais vite abandonné car trop compliqué à utiliser vu le nombre de messages à envoyer.
